算法基础

提醒

  1. 对于急需找工作的情况，建议优先刷leetcode的hot100题，而对于绝大多数的求职者来说，我们的算法能力只需要达到70-80左右即可，不要花大量的时间在算法上，而是有目的的学习
  2. 刷leetcode的最好时间是十年以前，其次就是现在。不能再堕落下去了，一定要出重拳！o(￣▽￣)o
  3. 既然我们的目的是70-80分，对于比较偏僻的知识点这里就不再提及(除非是面试中出现过的)

引自labuladong网站上的一句话

复习是一定需要的。我建议在刷完一个习题章节后，隔 3 天左右一定要再回来做一遍习题。

因为你之前已经过了一遍，所以复习时尽量不要看我的解法，自己思考求解。如果有做不出来的，那就看答案，然后过几天再回来做，直到都能求解出来为止。

切记不要背题

算法这个东西不是八股文，千万不要妄图背题，这样是没有用的。应该去理解算法的原理，而不是具体的解题代码。比方说，不要因为你记得上次这里使用的是 <= 号，所以回来复习的时候直接用 <=，这是没用的。

忘了题目的解法代码，这是好事啊，那你就自己分析，一边思考一边写嘛。为什么要用 <=，你要能说出个所以然来，这样才叫复习呀，否则就是囫囵吞枣死记硬背，没用的。会证明远比比会记忆更重要，一证胜万题

个人刷题感悟

  1. 任何数据结构，其特点既是它的优点也是它的缺点。比如数组的优点是连续，可以快速访问元素，缺点也是连续，扩容和增删时非常麻烦。
  2. 时间复杂度和空间复杂度对立统一，有得便有舍。
  3. 对于分治法的最好理解是"树上只有一片叶子，和剩下的叶子"
  4. 计算机的思维在于科学的穷举，穷举是所有算法题的最终解法。
  5. 一开始千万不要陷入实现的细节，像做数学题一样，联想性质，定义，条件，一步步推理，作答。

数据结构的实现

建议读者可以买一本《大话数据结构》的书并将上面所有的代码敲一遍，再回头看以前写过的算法题会有不一样的感受，站主之前就是这么学习数据结构的，即使我不是计算机专业的，但是我敲过的代码不比科班的少<(￣︶￣)>

后面的算法和数据结构将不再参考国内的教材(因为太垃圾) ，如果读者在YouTube或者是MIT、伯克利大学看过对应的CS公开课(比如CS61A)，就会意识到国内和国外的计算机教育差距有多么大，为了以后的发展，建议优先选择国外教材和课程。

以下实现语言均为C++，其他语言的读者可以去labuladong的网站上找对应的代码实现。

静态数组与动态数组

本部分算法实现与例题解决实现代码链接：点击此处

相关的总结

  1. 为什么数组的索引从 0 开始？就是方便取地址。arr[0] 就是 arr 的首地址，从这个地址往后的 4 个字节(一个int变量的大小，也就是指针所指对象的大小)存储着第一个元素的值；arr[1] 就是 arr 的首地址加上 1 * 4 字节，也就是第二个元素的首地址，这个地址往后的 4 个字节存储着第二个元素的值。arr[2], arr[3] 以此类推(英文教材将其称为offset,也就是偏移量的意思)

  2. 因为数组的名字 arr 就指向整块内存的首地址，所以数组名 arr 就是一个指针。你直接取这个地址的值，就是第一个元素的值。也就是说，*arr 的值就是 arr[0]，即第一个元素的值。

  3. 为什么国内的教材常常用memset初始化数组？如果不用 memset 这类函数初始化数组的值，那么数组内的值是不确定的。因为 int arr[10] 这个语句只是请操作系统在内存中开辟了一块连续的内存空间，但是其中的内容你是不知道的。

示例：比如以下代码

1
2
3
4
5
6
int main()
{
    int a;
    printf("%d",a);
    return 0;
}

在VS中会报错提示“使用了未初始化的内存a",在其他编译器可能能运行并打印一个比较大的值(不唯一)。

动态数组

动态数组底层还是静态数组，只是自动帮我们进行数组空间的扩缩容，并把增删查改操作进行了封装，让我们使用起来更方便而已。比如C++中的vector容器。虽然国内的教材喜欢用指针来实现动态数组，但其本质仍然是静态数组。

建议看我的这个动态数组的实现，有助于真正理解数据结构与算法的精髓。放心都有注释(❁´◡`❁) 点击此处

单链表与双链表

常见的用C++定义的链表如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class ListNode
{
public:
	int val;//节点的数据域，相当于data
	ListNode* next;
	ListNode(int x) :val(x), next(NULL) {} //显式初始化函数

//实际常用的链表节点
private:
	template<typename E>
	class Node
	{
	public:
		E val;
		Node* next;
		Node* prev;

		Node(Node* prev, E element, Node* next)
		{
			this->val = element;
			this->next = next;
			this->prev = prev;
		}
	};
};

需要注意的是，国内的教材喜欢用宏定义(比如ElemType)，让你可以指定val为任意数据类型，而在C++中有泛型编程的特性，可以用template实现。

常见的单链表和双链表操作如下，核心在于理解，而不是背变量名或者是代码，只要理解了想怎么命名都行。点击此处

循环数组

需要注意的是，循环数组的本质是数组，通过start和end”指针”最大限制利用分配的连续的空间。当 start, end 移动超出数组边界（< 0 或 >= arr.length）时，我们可以通过求模运算 % 让它们转一圈到数组头部或尾部继续工作，这样就实现了环形数组的效果，其他的全是实现的具体细节，完全可以自行推导，本质就这样，不要死背代码，真正理解内核才能一招破万题。

以下是实现的具体代码，可供参考

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
#pragma once
#include <stdexcept>
#include <ostream>

//循环数组的实现
template<typename T>
class CycleArray
{
	//成员变量
	unique_ptr<T[]> arr;//C++11特性，智能指针，会自动释放指针的内存
	int start;//头指针，指向第一个元素
	int end;//尾指针，指向最后一个元素的"下一位"
	int count;//元素数量
	int size;

	//自动扩缩容辅助函数
	void resize(int newSize)
	{
		//创建新的数组
		unique_ptr<T[]> newArr = make_unique<T[]>(newSize);
		//将旧数组的元素复制到新数组中
		for (int i = 0; i < count; i++)
		{
			newArr[i] = arr[(start + i) % size];//循环数组的核心在于取模实现"循环",每一次元素的增减都需要这一步
		}
		
		arr = move(newArr);
		//重置start与end指针
		start = 0;
		end = count;
		size = newSize;

	}

public:
	//循环数组的构造函数
	CycleArray() : CycleArray(1)
	{

	}

	//初始化时首尾指针指向同一个元素
	explicit CycleArray(int size) :start(0), count(0), size(size)
	{
		arr = make_unique<T[]>(size);
	}

	//在数组头部添加元素,时间复杂度为O(1)
	void addFirst(const T& val)
	{
		//当数组满时，扩容为原来的两倍
		if (isFull())
		{
			resize(size * 2);
		}
		//因为start是闭区间(这里设置为左闭右开，比如[0,0)代表初始没有元素),所以先左移，再赋值
		start = (start - 1 + size) % size;
		arr[start] = val;
		count++;
	}

	//删除数组头部元素，时间复杂度为O(1)
	void removeFirst(void)
	{
		//如果数组为空
		if (isEmpty())
		{
			throw std::runtime_error("Array is empty");
		}
		//先赋值，后右移
		arr[start] = T();
		start = (start + 1) % size;
		count--;
		//如果数组元素数量减少到原来大小的四分之一,则减少数组到原来大小的一半
		if (count > 0 && count == size)
		{
			resize(size/2);
		}

	}


	//在数组尾部添加元素，时间复杂度为O(1)
	void addLast(const T& val)
	{
		if (isFull())
		{
			resize(size * 2);
		}
		//end是开区间，所以先赋值，然后右移动一位
		//防止end成为负数，需要加上模数然后再取模
		arr[end] = val;
		end = (end + 1) % size;
		count++;
	}

	//删除数组尾部元素
	void removeLast()
	{
		if (isEmpty())
		{
			throw std::runtime_error("Array is empty");
		}
		//先移动再赋值，因为此时end是指向最后一个元素的"后一位"的
		end = (end - 1+size) % size;
		arr[end] = T();

		count--;
		//缩容
		if (count > 0 && count == size / 4)
		{
			resize(size / 2);
		}
	}

	//获取数组的头部元素
	T getFirst() const
	{
		if (isEmpty())
		{
			throw std::runtime_error("Array is empty");
		}
		return arr[start];
	}

	//获取数组尾部元素
	T getLast() const
	{
		if (isEmpty())
		{
			throw std::runtime_error("Array is empty");
		}
		return arr[(end - 1 + size) % size];
	}

	//判断数组是否已满
	//数据结构中经常使用start与end之间的关系判断循环数组是否已满或者是为空
	bool isFull() const
	{
		return count == size;
	}

	//判断数组是否为空
	bool isEmpty() const
	{
		return count == 0;
	}

	//获取循环数组的元素个数
	int getSize() const
	{
		return count;
	}
};

队列与栈

【概念】：队列和栈都是「操作受限」的数据结构，比如队列只能一端删除，一端添加。需要注意的是受限不是劣势，反而如果选择恰当，表现能比全能的数据结构还要出色。

相关的实现代码如下：点击此处

哈希表

【概念】：需要注意的是：哈希表和我们常说的 Map（键值映射)不是一个东西。

这一点用 Java 来讲解就很清楚，Map 是一个 Java 接口，仅仅声明了若干个方法，并没有给出方法的具体实现：

1
2
3
4
5
6
interface Map<K, V> {
    V get(K key);
    void put(K key, V value);
    V remove(K key);
    // ...
}

Map 接口本身只定义了键值映射的一系列操作，HashMap 这种数据结构根据自身特点实现了这些操作。还有其他数据结构也实现了这个接口，比如 TreeMap、LinkedHashMap 等等。也就是说，哈希表是map的一种实现方案。不要将map与哈希表混为一谈，也不要单纯认为查找的时间复杂度一定就是O(1),还是要看具体实现。

【实现】：哈希表的底层实现就是一个数组（我们不妨称之为 table）。它先把这个 key 通过一个哈希函数（我们不妨称之为 hash）转化成数组里面的索引，然后增删查改操作和数组基本相同。

为什么key是唯一的，但是value可以不唯一？因为哈希表通过哈希函数把 key 转化成 table 中的合法索引，才能实现时间复杂度为O(1)的查找，如果同一个键有多个，那么求出来的同一个索引就有多个，就会发生冲突。

相关的实现代码如下：点击此处

哈希函数索引合法化

一般来讲，索引是正值，以数学的角度很容易想到一旦算出的结果为负值的时候就取反，类似这样

1
2
int h = key.hashCode();
if (h < 0) h = -h;

对吗？不对 因为int 类型可以表示的最小值是 -2^31，而最大值是 2^31 - 1。所以如果 h = -2^31，那么 -h = 2^31 就会超出 int 类型的最大值，这叫做整型溢出，编译器会报错。

那么如何解决呢？可以利补码编码的原理，直接把最高位的符号位变成 0

1
2
3
4
5
6
7
8
int h = key.hashCode();
// 位运算，把最高位的符号位去掉
// 另外，位运算的运行速度也会比一般的算术运算快
// 所以你看标准库的源码，能用位运算的地方它都会优先使用位运算
h = h & 0x7fffffff;
// 这个 0x7fffffff 的二进制表示是 0111 1111 ... 1111
// 即除了最高位（符号位）是 0，其他位都是 1
// 把 0x7fffffff 和其他 int 进行 & 运算之后，最高位（符号位）就会被清零，即保证了 h 是非负数

负载因子

【概念】：负载因子是一个哈希表装满的程度的度量。一般来说，负载因子越大，说明哈希表里面存储的键值对越多，哈希冲突的概率就越大，哈希表的操作性能就越差。如果我们需要自己设计一个哈希函数，就需要考虑到在负载因子增大的时候扩容，防止冲突的概率变大。

键值对的注意事项

【建议或者强制】：键应该是不可变数据类型，否则对键值的修改会导致映射的索引变化，甚至会导致键值对丢失的问题。

拉链法的实现相关的实现代码如下：点击此处

线性探测法

注意事项

  1. labuladong说线性探查法的删除操作比较复杂，因为要维护元素的连续性。关键在于以下代码
1
2
3
4
5
6
7
8
9
10
11
int get(int key) {
        int index = hash(key);
        // 向后探查，直到找到 key 或者找到空位
        while (index < 10 && table[index] != nullptr && table[index]->key != key) {
            index++;
        }
        if (index >= 10 || table[index] == nullptr) {
            return -1;
        }
        return table[index]->value;
}

一旦多个键值对哈希冲突并使用线性探测法时，它们的索引关系就是“连续的”。比如

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//代码部分
put(0, a)
put(10, b)
put(20, c)

put(3, A)
put(13, B)

put(30, d)
put(40, e)

//示意图

table = [a, b, c, A, B, d, e, _, _, _]
index    0  1  2  3  4  5  6  7  8  9
hash     ^        ^
key      0 10 20  3 13  30 40

这里a、b、c都是在索引0处哈希冲突并使用线性探测法匹配到自己的索引，分别是0，1，2,如果我们将b的键值对删除，那么就会导致a与c之间存在nullptr，而get函数的逻辑是一旦遇到nullptr就会停止并返回-1，就会导致明明存在但无法找到的情况，所以必须保证连续性

【实现】：两种实现的细节要注意，一个是探测的函数，是向前后移动？移动多少？都是可以优化的地方。另一个是涉及到增删操作，如何保证连续也是一个问题。

具体实现代码如下：点击此处

二叉树

最重要的数据结构之一，是理解树相关的算法和图相关算法的基础和前提。

【概念】：中文的概念这里不再赘述，需要注意的是在英文中Complete Binary Tree对应的是完全二叉树，而 Perfect Binary Tree。对应的是满二叉树。Full Binary Tree是指一棵二叉树的所有节点要么没有孩子节点，要么有两个孩子节点，如果英语直译的话很容易翻译成满二叉树，而实际上不是。

二叉树的遍历

  1. 不管学校里教的，刷题刷的，还是算法导论里面写的，核心就一句话。递归遍历节点的顺序仅取决于左右子节点的递归调用顺序，与其他代码无关。也就是以下代码
1
2
3
4
5
6
7
8
9
10
void traverse(TreeNode* root)
{
	if (root == nullptr)
	{
		return;
	}
    //这两个左右子节点递归调用的顺序决定了遍历节点的顺序，与什么printf函数均无关
	traverse(root->left);
	traverse(root->right);
}
  1. 学过数据结构的读者会认为顺序不是有前中后序和层序遍历吗？是的，不过我们的输出函数是穿插在这两个节点调用函数中的，当然会有不同的效果，如下
1
2
3
4
5
6
7
8
9
10
11
12
void traverse(TreeNode* root)
{
	if (root == nullptr)
	{
		return;
	}
	//前序遍历的位置，数据结构中就喜欢在这里写一个printf(e) 其中e为节点的值
	traverse(root->left);
	//中序遍历，同理写printf函数
	traverse(root->right);
	//后序遍历
}

具体实现代码如下：点击此处

多叉树的递归和遍历

【数据结构】在leetcode中基本上和二叉树的结构一样，就只是类型变成了vector 用于存放节点的数组

1
2
3
4
5
6
class Node
{
public:
    int val;
    vector<Node*>children;
};

【常见的算法】

  1. 对于多叉树来说，前中后序遍历失去了意义，但是还有层序遍历可以实现，这也是多叉树常用的遍历算法，仅次于DFS与BFS。示例如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
//N叉树的层序遍历
//方法1 借助队列
void levelOrderTraverse1(Node* root)
{
    if (root == nullptr)
    {
        return;
    }
    std::queue<Node*> q;
    q.push(root);

    while (!q.empty())
    {
        Node* cur = q.front();
        q.pop();
        //访问cur节点
        std::cout << cur->val << std::endl;

        //把cur所有子节点加入队列
        for (Node* child : cur->children)
        {
            q.push(child);
        }
    }
}


//方法2 记录节点深度
void levelOrderTraverse(Node* root)
{
    if (root == nullptr)
    {
        return;
    }

    std::queue<Node*> q;
    q.push(root);
    int depth = 1;
    while (!q.empty())
    {
        int sz = q.size();
        for (int i = 0; i < sz; i++)
        {
            Node* cur = q.front();
            q.pop();

            //访问cur节点，同时知道他所在的层数
            cout << "depth = " << depth << ", val = " << cur->val << endl;

            for (Node* child : cur->children)
            {
                q.push(child);
            }
        }
    }
}


//方法3 记录权重
//带权重的树节点
class State
{
public:
    Node* node;
    int depth;

    State(Node* node, int dept) :node(node), depth(depth) {};
};


void levelOrderTraverse3(Node* root)
{
    if (root == nullptr)
    {
        return;
    }

    std::queue<State>q;
    q.push(State(root,1));

    while (!q.empty())
    {
        State state = q.front();
        q.pop();

        Node* cur = state.node;
        int depth = state.depth;

        //访问节点
        cout << "depth = " << depth << ", val = " << cur->val << endl;

        //进入子节点，注意深度+1
        for (Node* child : cur->children)
        {
            q.push(State(child,depth+1));
        }
    }
}

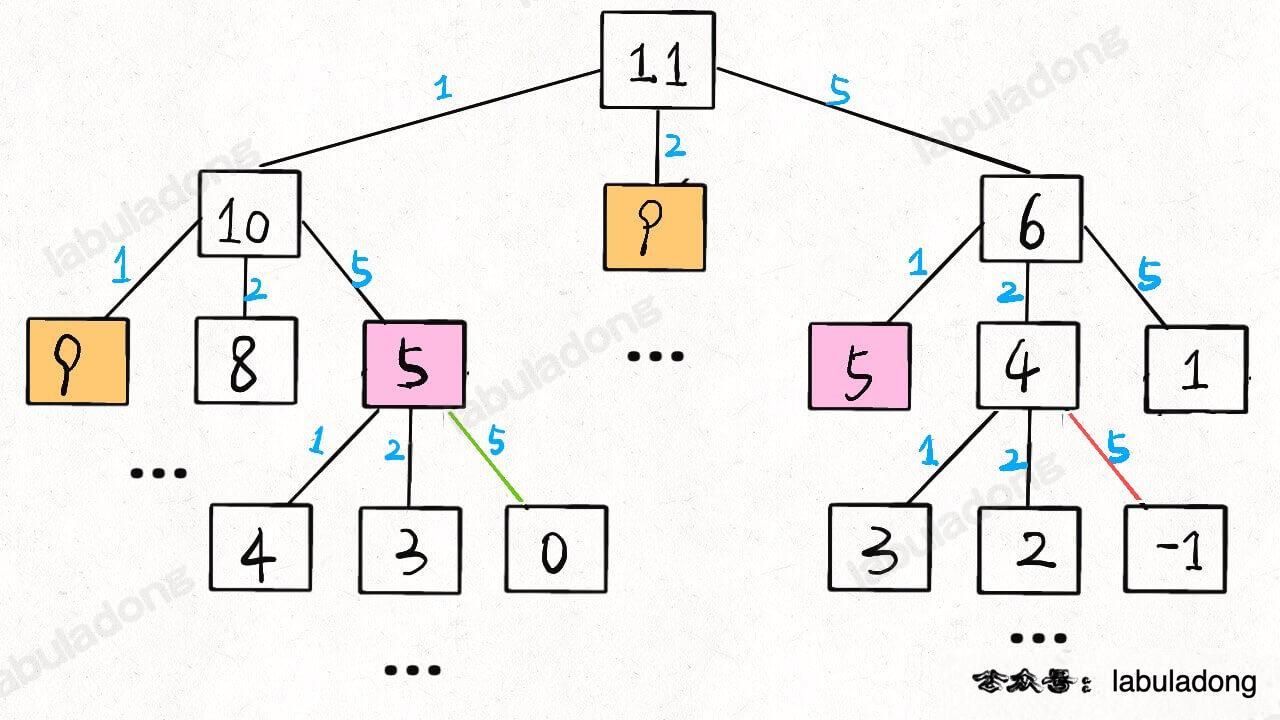
字典树

【数据结构】：和多叉树一样，不同的是一般用孩子数组的索引代表一个字符。的值.示例代码如下。

1
2
3
4
5
6
7
template<typename V>
struct TrieNode
{
	V val = NULL;//val是键所对应的值
	TRieNode<v>* children[256] = { NULL };//这里索引代表键中的一个字符，可以避免重复存储相同的前缀和
	//这也是字典树被称为前缀树的原因
};

示意图如下(引用labuladong网站上的图)：

其中白色节点代表 val 字段为空，橙色节点代表 val 字段非空。用树枝(也就是连线)表示字符。这样就能共享前缀，从而减少大量的存储空间消耗

如果读者对数据结构足够了解的话，会发现和霍夫曼树有几分相似之处。没错，霍夫曼树差不多是相反的，是避免一个二进制串是另一个二进制串的前缀。

具体实现代码如下：点击此处

二叉堆

【数据结构】：本质是二叉树，其中优先级队列可以用数组的存储结构实现，示例如下.

注意优先级队列本质是树，对于任何一个节点，都大于(或者小于)其子节点。每次插入或者删除都会自动调整树的结构。使其保持二叉堆的特性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
#pragma once
#include <vector>
#include <functional>
#include <stdexcept>
#include <iostream>
using namespace std;

//优先级队列的实现-用数组的存储结构，和树的逻辑结构实现
//前提是完全二叉树，因为完全二叉树元素是连续的，可以用数组连续的排放
template <typename T>
class MyPriorityQueue
{
private:
	//堆数组
	std::vector<T>heap;

	//堆中元素的数量
	int size;

	//元素比较器
	std::function<bool(const T&, const T&)> comparator;

	//父节点的索引
	//规律和二叉树的一样，这里索引从0开始
	//自己列一个数组然后推理就行，和数据结构中左右孩子节点求法还是不一样的
	int parent(int node)
	{
		return (node - 1) / 2;
	}

	//左孩子节点的索引
	int left(int node)
	{
		return node * 2 + 1;
	}

	//右孩子节点的索引
	int right(int node)
	{
		return node * 2 + 2;
	}

	//交换数组的两个元素
	void swap(int i, int j)
	{
		std::swap(heap[i], heap[j]);
	}

	//调整堆的大小
	void resize(int capacity)
	{
		if (capacity > size)
		{
			heap.resize(capacity);
		}
	}


	//上浮操作，时间复杂度是树高O(logn)
	//持续追踪一个节点，直到其上浮到合适的位置
	void swim(int node)
	{
		//如果节点比父节点值要小
		while (node > 0 && comparator(heap[parent(node)], heap[node]))
		{
			swap(parent(node), node);
			node = parent(node);
		}
	}

	//下沉操作，时间复杂度为树高O(logN)
	void sink(int node)
	{
		while (left(node) < size || right(node) < size)
		{
			//比较自己的左右子节点，找最小值
			int min = node;
			if (left(node) < size && comparator(heap[min], heap[left(node)]))
			{
				min = left(node);
			}
			if (right(node) < size && comparator(heap[min], heap[right(node)]))
			{
				min = right(node);
			}
			//如果当前节点比子节点都小
			if (min == node)
			{
				break;
			}

			//与最小值交换
			swap(node, min);
			//继续下沉
			node = min;
		}
	}
public:
	//构造函数
	MyPriorityQueue(int capacity, std::function<bool(const T&, const T&)>compator)
		:heap(capacity), size(0), comparator(std::move(compator)) {};

	//返回堆的大小
	int getSize() const
	{
		return size;
	}

	//判断堆是否为空
	bool isEmpty() const
	{
		return size == 0;
	}

	//查找元素,返回堆顶的元素，其时间复杂度是O(1)
	const T& peek() const
	{
		if (isEmpty())
		{
			throw std::underflow_error("Priority queue underflow");
		}
		return heap[0];
	}

	//向堆中插入一个元素，时间复杂度为O(logN)
	void push(const T& x)
	{
		//扩容
		if (size == heap.size())
		{
			resize(2 * heap.size());
		}
		//把新元素追加到最后
		heap[size] = x;
		//然后上浮,传入的参数为数组的索引
		swim(size);
		size++;
	}

	//删除堆顶元素，时间复杂度为O(logN)
	T pop()
	{
		if (isEmpty())
		{
			throw std::underflow_error("PriorityQueue underflow");
		}
		T res = heap[0];
		//把堆底元素放在堆顶
		swap(0, size - 1);
		size--;
		//然后下沉到正确的位置
		sink(0);
		//缩容
		if (size > 0 && size == heap.size() / 4)
		{
			resize(heap.size() / 2);
		}
		return res;
	}
};


void Test_PriorityQueue(void)
{
	// 使用lambda表达式来传递比较器
	// 小顶堆
	MyPriorityQueue<int> pq(3, [](const int& a, const int& b) { return a > b; });
	pq.push(3);
	pq.push(1);
	pq.push(4);
	pq.push(1);
	pq.push(5);
	pq.push(9);

	// 1 1 3 4 5 9
	while (!pq.isEmpty()) {
		std::cout << pq.pop() << " ";
	}
	std::cout << std::endl;
}

线段树

【数据结构】：其特点是叶子节点是区间上具体一点的值，而从根节点到非叶子节点都是区间的二分。比如根节点是[0,11],其左右孩子分别是[0,5],[6,11]，相应的左右孩子又分别是[0,2],[3,5],[6,8],[8,11],也就是[left,mid],[mid,right]，其中mid = (left+right)/2 向下取整。这里的非叶子节点相当于索引，用于快速计算出区间的和等。

排序

选择排序

如果你学过排序，请忘掉你背过的代码，作为一个没有学过编程的学生去想，对于一组数据，如何从小到大排序。

你的第一反应就是穷举，也就是每次从未排序的集合中找出最小的放在前面，然后再对剩下的重复此操作。这就是选择排序

示例代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#pragma once
#include <iostream>
#include <vector>

using namespace std;

//选择排序的实现
//时间复杂度为O(n^2)
void sort(vector<int>& nums)
{
	int n = nums.size();
	//其中sortedIndex是一个分割线
	//索引 < sortedIndex的元素都是已经排序后的
	//索引 >= sortedIndex的元素都是未排序的
	int sortedIndex = 0;//初始化为所有元素都没有排序
	while (sortedIndex < n)
	{
		//先找到[sortedIndex,n)中的最小值
		int minIndex = sortedIndex;
		for (int i = sortedIndex + 1; i < n; i++)
		{
			if (nums[i] < nums[minIndex])
			{
				minIndex = i;
			}
		}
		//交换最小值和sortedIndex处的元素
		int temp = nums[sortedIndex];
		nums[sortedIndex] = nums[minIndex];
		nums[minIndex] = temp;

		sortedIndex++;
	}
}

选择排序的优化

优化的重点是不稳定的排序，核心在于交换后元素之间的相对顺序改变了——比如2 2`本来2` 应该在2的后面(后一位两位都行，如果要求在确定的一位就是绝对顺序)，但是选择排序交换之后就变成2` 2 这样，就破坏了相对顺序。解决问题的关键在于不要将确定后的最小值交换回去。而是用数组中间插入元素的思路，给sortedIndex索引后一位留空，等待下一个最小值填充。

常见的算法刷题框架

有几句话我要写在这里，对于算法的理解非常贴切。均来自labuladong的算法笔记，在未来的刷题过程中会深刻体会到这些道理。

种种数据结构，皆为数组（顺序存储）和链表（链式存储）的变换。

数据结构的关键点在于遍历和访问，即增删查改等基本操作。

种种算法，皆为穷举。

穷举的关键点在于无遗漏和无冗余。熟练掌握算法框架，可以做到无遗漏；充分利用信息，可以做到无冗余。

双指针

  1. 【推荐】在链表中建议使用虚拟头节点技巧，可以规避额外处理的情况(比如空指针，越界的情况)

正例：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        //使用双指针技巧解决链表问题
        ListNode dummy(-1);//创建一个链表，而且使用虚拟头节点的方式
        ListNode *p = &dummy;
        
        //代码逻辑部分
        
        return dummy.next;//由于使用了虚拟头节点，所以要返回头节点的下一个节点指针
    }
}

反例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* p1 = head;
        ListNode* p2 = head;
        for(int i = 0;i<n-1;i++)
        {
            p1 = p1->next;
        }

        //然后开始移动第二个指针
        while(p1!=nullptr)
        {
            p1 = p1->next;
            p2 = p2->next;
        }

        //此时p2移动到指定位置的上一个位置，方便删除
        p2->next = p2->next->next;
//Line 19: Char 30: runtime error: member access within null pointer of type 'ListNode' (solution.cpp)
//SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior prog_joined.cpp:39:30

        return head;

    }
};

19行出现错误，访问了空指针不存在的成员类型。

  1. 【建议】：涉及到指针的内存需要释放和指针的指向，建议释放并将其置空

正例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        ListNode* slow = head;
        // 释放slow后面剩余的重复节点
        ListNode* temp = slow->next;
        while(temp != nullptr) {
            ListNode* toDelete = temp;
            temp = temp->next;
            delete toDelete;//1. 释放不需要的内存
            toDelete = nullptr;//2. 将指针置空
        }
        slow->next = nullptr;

        return head;
    }
};
  1. 【总结】：双指针只是一种形式，以不同的方式移动它就可以达到不同的效果，比如一个指针总是指向极值，另一个指针指向容器，就可以按顺序排列元素，或者分离，或者合并；一个指针快，一个指针慢，如果在”环“(无论是逻辑上的还是物理上的)上移动，就可以相遇；如果有条件的移动，就可以窗口一样筛选；是从一边移动？还是中心开花？还是从两侧向中间靠拢？都是可以研究的对象。关键在于移动的条件是什么？从哪里移动？是先操作再移动？

二分查找

一句话概括：思路很简单，细节是魔鬼。

【实现】：常见的框架如下所示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int binarySearch(vector<int>& nums, int target) {
    int left = 0, right = nums.size() - 1;

    while (...) {//这里写终止二分搜索的判断语句
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ...//一般搜索到到目标函数就直接返回，不过要视题目而定
        } else if (nums[mid] < target) {
            left = ...//左指针如何移动
        } else if (nums[mid] > target) {
            right = ...//右指针如何移动
        }
    }
}

需要说明的是，在数据结构中mid是这样计算的

1
int mid = (left+right)/2;

而在实际的算法题中，计算 mid 时需要防止溢出，代码中 left + (right - left) / 2 就可以防止left和right太大导致溢出的情况。

推理如右:a+b2=b−a+2×a2=a+b−a2\frac{a+b}{2} = \frac{b-a+2 \times a}{2} = a+\frac{b-a}{2}

while中的判断一般有两种常见的形式：left<right 和left<=right

区别在于你初始化的right是什么，比如你初始化为int right = nums.size(); 本身right超出了数组索引的边界，相当于是[left,right) 左闭右开区间，当left = right时，此时[left,left) 而left<right的终止条件是left == right.可以正确终止;left<=right同理

left和right“指针”的修改:

在while判断条件下left<right ，为什么是right = mid？同理，因为搜索区间是左闭右开，当mid被检测之后，下一步应该去mid的左侧或者右侧区间搜索，即[left,mid) 和[mid+1,right) 所以mid可以==right,left可以为mid+1;

以下是labuladong提供的二分查找的左右闭合区间的框架。如果 target 不存在，搜索左侧边界的二分搜索返回的索引是大于 target 的最小索引。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int left_bound(vector<int>& nums, int target) {
    int left = 0, right = nums.size() - 1;
    // 搜索区间为 [left, right]
    while (left <= right) {//终止条件是left == right+1
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            // 搜索区间变为 [mid+1, right]
            left = mid + 1;
        } else if (nums[mid] > target) {
            // 搜索区间变为 [left, mid-1]
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 收缩右侧边界
            right = mid - 1;
        }
    }
    // 判断 target 是否存在于 nums 中
    // 如果越界，target 肯定不存在，返回 -1
    if (left < 0 || left >= nums.size()) {
        return -1;
    }
    // 判断一下 nums[left] 是不是 target
    return nums[left] == target ? left : -1;
}

动态规划

【三要素】：重叠子问题、最优子结构、状态转移方程，在后续的解题中都是围绕这些展开的

来自labuladong的框架。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 自顶向下递归的动态规划
# 定义了一个方程
def dp(状态1, 状态2, ...):
    for 选择 in 所有可能的选择:
        # 此时的状态已经因为做了选择而改变
        result = 求最值(result, dp(状态1, 状态2, ...))
    return result

# 自底向上迭代的动态规划
# 初始化 base case
dp[0][0][...] = base case
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

如何理解重叠子问题？以最经典的斐波那契数列为例，常见的暴力算法如下

1
2
3
4
int fib(int N) {
    if (N == 1 || N == 2) return 1;
    return fib(N - 1) + fib(N - 2);
}

其时间复杂度为子问题 * 一个子问题所需要的时间，用递归树理解就是树中有2n2^{n} 个节点，每一个节点的时间复杂度为O(1),两者相乘为指数级别的时间复杂度。为什么会这样呢？就是因为树中存在大量重复计算，比如求f(5)，f(5)的子问题是f(4)与f(3)，f(4)的子问题是f(3)与f(2),其中f(3)被重复计算了两次，如果树更高，重复计算的次数只会更多，这就是重复的子问题。

而对于这种重复的子问题，一种常见的解决思路是备忘录，也就是将计算过的结果记录下来，下次计算前如果发现备忘录中已经有了，就不需要重复递归计算了，示例代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int fib(int n) {
        //备忘录初始化为0
        vector<int> memo(N+1,0);
        //带备忘录的递归
        return dp(memo,N);
    }

    //带备忘录递归
    int dp(vector<int>&memo,int n)
    {
        if(n == 0 || n == 1)
        {
            return n;
        }
        if(memo[n]!=0)
        {
            return memo[n];
        }
        memo = dp(memo,n-1)+dp(memo,n-2);
        return memo[n];
    }
};

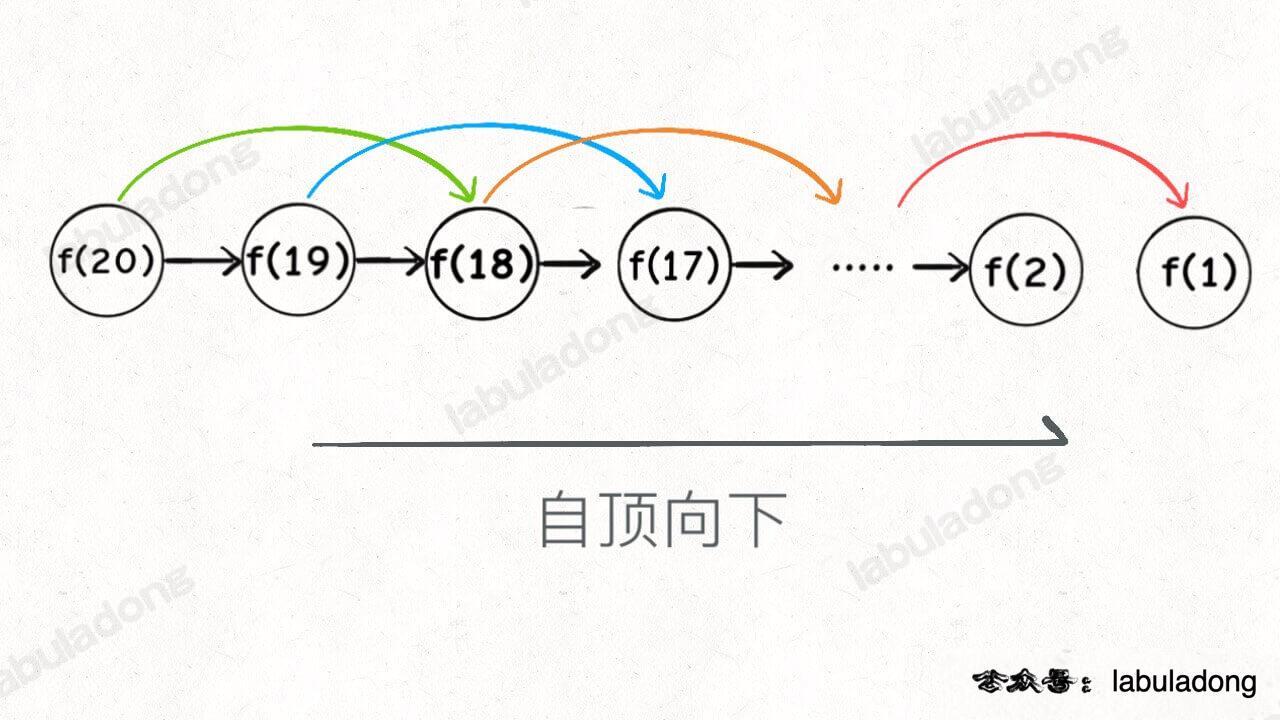
通过备忘录将递归树剪枝，大大减少了冗余计算，示例图如下，来自labuladong的网站

由此可以看出，递归的思路一般是自顶向下，而动态规划恰恰相反，是从最简单的问题开始，一步步向上推，所以你会看到几乎大部分的动态规划都是借助循环遍历实现的。

递归的思路反过来就是动态规划，示例如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int fib(int n)
{
    if(n == 0)
    {
        return 0;
    }
    //创建一个备忘录数组
    vector<int> dp(n+1);
    dp[0] = 0,dp[1] = 1;
    //开始状态转移，也就是自底向上
    for(int i = 2;i<=n;i++)
    {
        dp[i] = dp[i-1]+dp[i-2];
    }
    
    return dp[n];
}

什么是状态转移方程？其实就是描述问题的函数，一般是分段函数，如下

f(n)={1n=1,2f(n−1)+f(n−2)n>2f(n) = \begin{cases} 1 & n = 1,2 \\ f(n-1)+f(n-2)& n>2 \end{cases}

把参数 n 当做一个状态，这个状态 n 是由状态 n - 1 和状态 n - 2 转移（相加）而来，这就叫状态转移。

状态转移方程往往是动态规划最关键的一步，其他什么备忘录等只是在此基础上进行优化而已。

在上述代码的基础上，我们发现n状态只与n-1和n-2有关，那么就可以想到可以只保留n-1与n-2而不需要那么多的空间，只要记得每次刷新就行，最终得到的斐波那契的动态规划如下.如果在实际情况下发现只需要DP table中的一部分，就可以尝试缩小其大小

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int fib(int n) {
    if (n == 0 || n == 1) {
        // base case
        return n;
    }
    // 分别代表 dp[i - 1] 和 dp[i - 2]
    int dp_i_1 = 1, dp_i_2 = 0;
    for (int i = 2; i <= n; i++) {
        // dp[i] = dp[i - 1] + dp[i - 2];
        int dp_i = dp_i_1 + dp_i_2;//先记录得到的i状态
        // 滚动更新
        dp_i_2 = dp_i_1;//
        dp_i_1 = dp_i;
    }
    return dp_i_1;
}

什么叫最优子结构？专业来说就是子问题互相独立，简单来说有点像贪心，比如要总分要高就要每科都要考高分，而每个科目成绩相互独立，互不影响，就叫最优子结构。一旦破坏了这种关系(比如数学考的高，英语就低)，这种情况下就不能简单的认为只要每科高就能实现总分高了。

比如凑零钱问题，常见的实现代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        // 题目要求的最终结果是 dp(amount)
        return dp(coins, amount);
    }

private:
    // 定义：要凑出金额 n，至少要 dp(coins, n) 个硬币
    int dp(vector<int>& coins, int amount) {
        // base case
        if (amount == 0) return 0;
        if (amount < 0) return -1;

        int res = INT_MAX;
        for (int coin : coins) {
            // 计算子问题的结果
            int subProblem = dp(coins, amount - coin);
            // 子问题无解则跳过
            if (subProblem == -1) continue;
            // 在子问题中选择最优解，然后加一
            res = min(res, subProblem + 1);
        }

        return res == INT_MAX ? -1 : res;
    }
};

如果用labuladong给的递归树来解释的话，就是找到以金额amount为根节点，到某一个叶子节点值为0的点的最短路径(也就是从根到此叶子节点的深度-1)。建议一定要掌握画递归树，有助于理解动态规划的三要素。

反过来就是动态规划的代码了，示例如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        //dp[i]数组的定义是，凑出金额为i所需要的最少的硬币数量
        //将其每个值初始化为amount+1，因为凑出amount最多需要amount个1元，将其视作正无穷，防止溢出
        vector<int>dp(amount+1,amount+1);

        //开始状态转移
        //dp数组第一位为0,实际根据题目改变
        dp[0] = 0;
        for(int i = 0;i<dp.size();i++)
        {
            for(auto coin:coins)
            {
                //如果无解就跳过
                if(i-coin<0)
                {
                    continue;
                }
                //状态转移方程
                dp[i] = min(dp[i],1+dp[i-coin]);
            }
        }
        
        //返回参数前进行判断，是否值为amount+1
        return (dp[amount] == amount+1)?-1:dp[amount];
    }
};

状态转移方程简单来说就是：dp[i]依赖于dp[i-1],dp[i-2]和dp[i-5] ,从中选择最小的那个，然后+1(要选一个硬币才能达到dp[i])。

二叉树系列

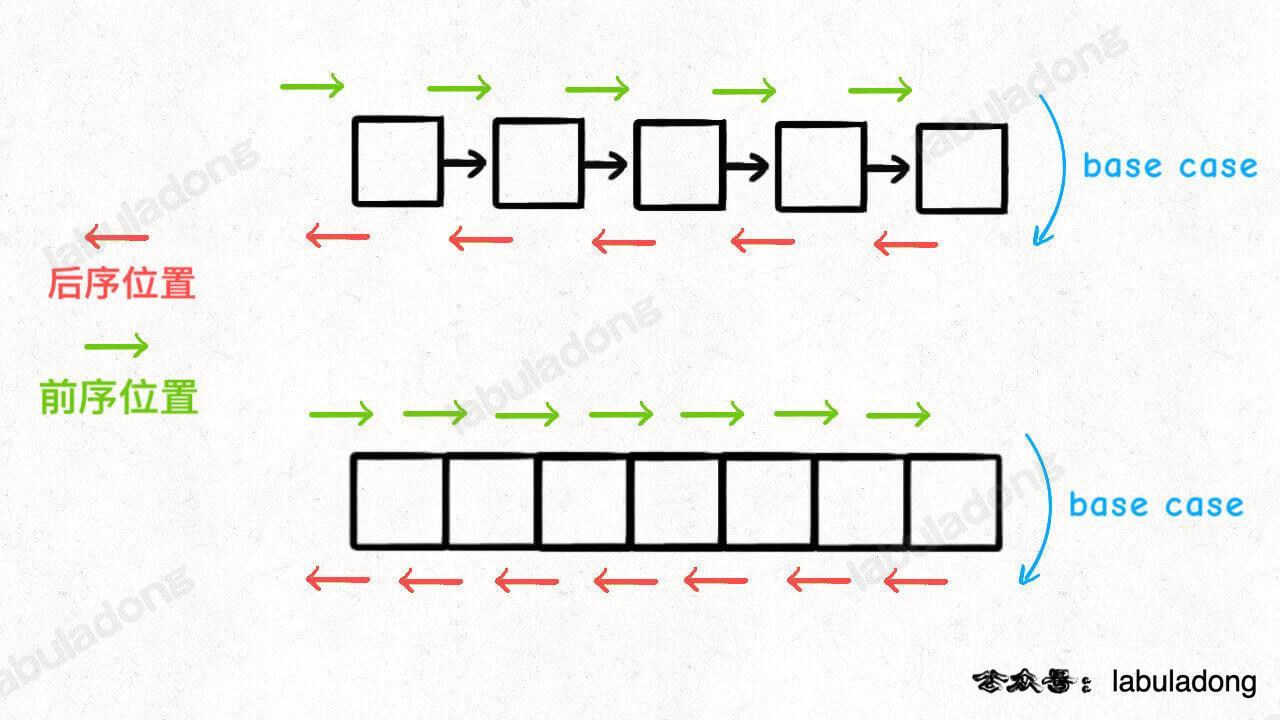
  1. 快速排序就是个二叉树的前序遍历，归并排序就是个二叉树的后序遍历
  2. 所谓前序位置，就是刚进入一个节点（元素）的时候，后序位置就是即将离开一个节点（元素）的时候 比如前序遍历时在进入traverse()函数的时候就是刚进入一个元素，离开traverse(right)函数要结束就是即将离开一个节点的时候

比如链表逆序打印，就是利用了递归的本质。先递归到链表尾部，在离开节点的时候再打印，也就是后序位置打印。

1
2
3
4
5
6
7
8
9
// 递归遍历单链表，倒序打印链表元素
void traverse(ListNode* head) {
    if (head == nullptr) {
        return;
    }
    traverse(head->next);
    // 后序位置
    cout << head->val << endl;
}

labuladong的图非常清晰，在数据结构中你也见到过，就是讲线索二叉树的时候画的进入和离开的线。

1.jpeg (1280×720)

  1. 二叉树的所有问题，就是让你在前中后序位置注入巧妙的代码逻辑，去达到自己的目的，你只需要单独思考每一个节点应该做什么，其他的不用你管，抛给二叉树遍历框架，递归会在所有节点上做相同的操作

动归/DFS/回溯算法都可以看做二叉树问题的扩展，只是它们的关注点不同：

  • 动态规划算法属于分解问题（分治）的思路，它的关注点在整棵「子树」。
  • 回溯算法属于遍历的思路，它的关注点在节点间的「树枝」。
  • DFS 算法属于遍历的思路，它的关注点在单个「节点」。

贪心算法

还记的之前的那个考试总分最高的例子吗？假设你参加高考，要考语数英物化生六门科目，其中每一门科目都有对应一系列的可选的分数，请输出一个序列，使得总分最高。

读者肯定能一眼看出答案，只要每个科目都选最高的，不就能使得总分最高了吗？这就是贪心的性质，能够通过局部最优解直接推导出全局最优解。

参考

  1. 力扣刷题攻略 读者可以在这里参考刷题。
  2. 本站简介 | labuladong 的算法笔记 建议没有思路的读者按照此网站目录刷题