算法系列(二)蓝桥杯_算法基础
算法基础
一放假就有点放纵自我了,不能再堕落下去了,一定要出重拳!o( ̄▽ ̄)o
目前以视频的方法为主,等蓝桥杯考完之后按照labuladong或者是考研的方法写代码。
我的仓库使用指南
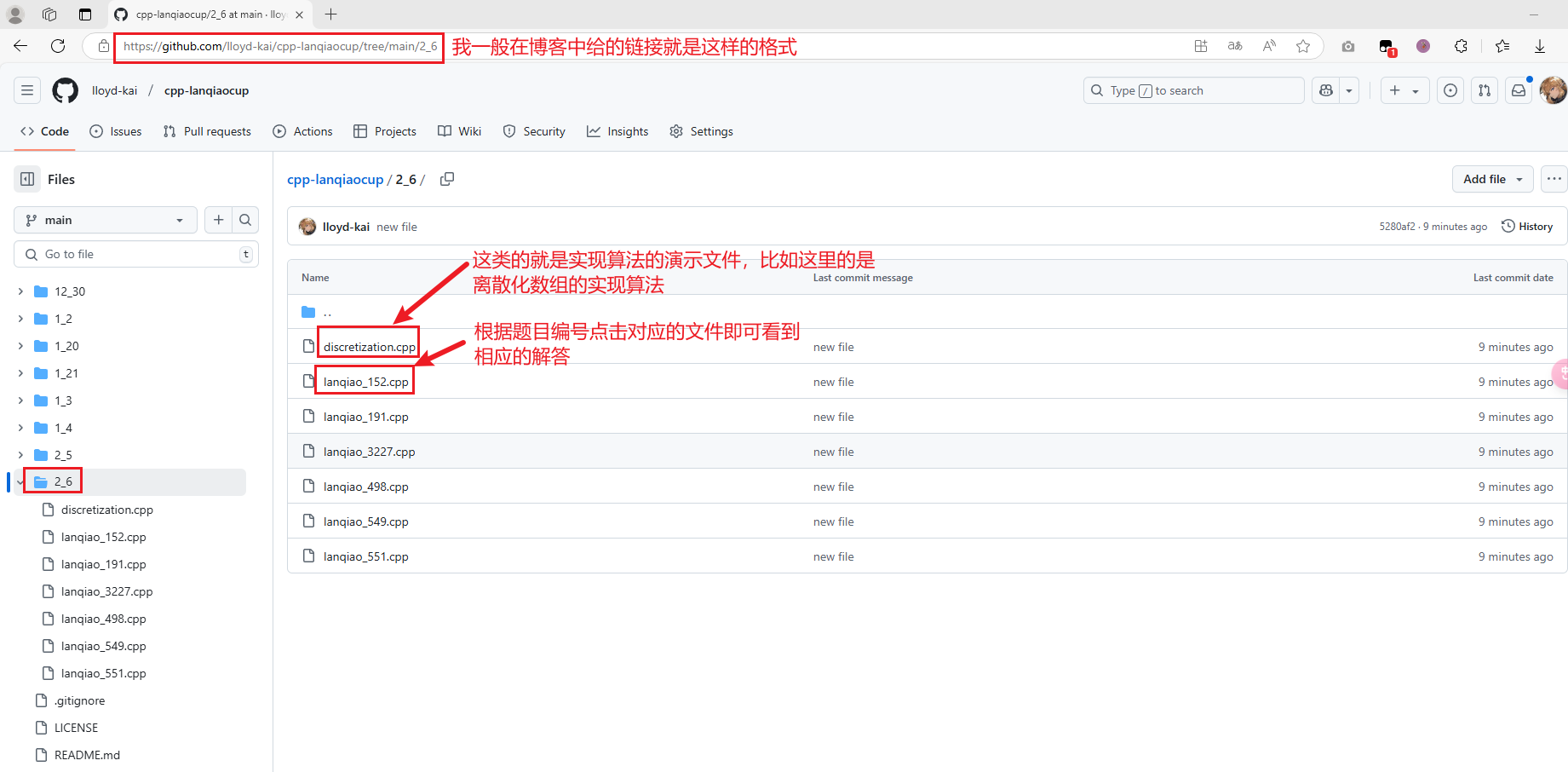
我的仓库链接格式如下:https://github.com/lloyd-kai/cpp-lanqiaocup/tree/main/1_20 其中1_20表示的是日期(一般是2025),里面的文件就包含对应题目的解答(均通过对应题目的测试)或者是算法实现,其中文件名lanqiao表示 是蓝桥杯官网上的题目,_ 后面的数字是蓝桥杯的题目编号,可以找到对应的蓝桥杯的题目,比如题目链接是https://www.lanqiao.cn/problems/498/learning/?page=1&first_category_id=1&problem_id=498 problems斜杠后面的数字498 就是对应的题目编号,你就在我指定链接下面的文件夹下按照lanqiao_题目编号.cpp 这样的格式找对应文件,就可以看到对应题目的解答代码。
差分数组
【概念】:diff[i] = a[i]-a[i-1];//对于数组a,diff为差分数组 当i=1时,diff[1]=a[1]
【性质】:对差分数组作前缀和可以将其转化为原数组。 公式:
利用差分数组可以实现快速的区间修改,下面是将区间[l,r]都加上X的方法:
1 | diff[l]+=x;//相当于a[l]-a[l-1] = x+原来的diff[l]; |
在修改完成后,需要做前缀和恢复为原数组,所以上面这段代码的含义是:diff[l]+=X表示将区间[l,n]都加上x,但是[r+1,n]我们并不想加x,所以再将[r+1,n]减去x即可。
这是怎么实现的呢?其实很简单,在通过前缀和恢复为原数组的时候,在区间的起始处+X,用公式计算在区间后面的数一定会加上这个值,比如a[l+1] = diff[1]+diff[2]+……+diff[l]+diff[l+1];而这里的diff[l]已经加上X了,这就是奥妙所在,而要想只加到r区间,那么同理就是在这个区间的后一个元素减去X(这里的区间是左右闭合),比如a[r+2] = diff[1]+diff[2]+……+diff[l]+……+diff[r]+diff[r+1]+diff[r+2];这里的diff[l]与diff[r+1]一加一减X正好抵消。
1 | for(int i = 1;i<=n;i++) |
【例题】
-
1.区间更新 - 蓝桥云课 难点:一是对于差分数组和前缀和性质的掌握,另一个是细节部分,比如对于数组的大小建议使用常数,cin获取输入作为while的判断条件,还有特定条件下输出空格或者是换行符。
-
1.小明的彩灯 - 蓝桥云课 如果不注意到数组越界和栈溢出的问题很容易无法通过测验。
【实践易错点】
在 int main 中,声明数组 int arr[N+1] 和 int diff[N+1] 可能会遇到的问题是由于栈内存的限制。栈内存的大小通常有限(在一些编译环境中,栈空间的大小是 1MB 左右)。如果在 main 函数内声明非常大的数组,可能会导致栈溢出错误。我在实际做题的时候就因为这个原因导致无法通过测验,也就提醒读者在初始化数组等不确定大小的数据结构时,尽可能将其在全局区域或者是堆区中事先初始化,以免出现栈溢出、数组越界等问题。
1 |
|
递归
相关知识点在算法系列(一)中讲解了,这里主要讲做题。
【例题】:输入n,求F(n)(F为斐波那契),其中n<=100000,结果对1e9+7(也就是1*10^9^ +7)取模
示例代码
1 |
|
【例题】
分析:正向看是(6)(1 6)(2 6)(1 2 6)(3 6)(1 3 6),但是从右往左看就是以6开头,其”分支“都是比其”根节点“的一半要小或者相等,这就容易想到使用dfs+递归的方式解决问题。当然只递归也可以实现。示例见此链接 。
二分
【概念】:是一种高效的查找方法,通过逐次将搜索范围一分为二,快速找到要查找的内容,适用于有序数据集合(这里的有序可以是正逆序,等差等比等以一定规律排序的方法)
常见的二分类型:整数二分,浮点二分,二分答案(最为常见)
【解题步骤】
- 研究并发现数据结构(或答案变量)的单调性。
- 确定最大区间[l,r],确保分界点一定在里面,具体有一些细节:若以r作为答案,那么答区间在[l+1,r],若以l作为答案,那么答案区间在[l,r-1]。
- 确定check函数,一般为传入mid(区间中某个下标),返回mid所属区域或返回一个值,当check函数较简单时可以直接判断
- 计算中点mid=(l+r)/2,用check判断该移动l或r指针,具体移动哪个需要根据单调性以及要求的答案来判断。
- 返回l或r,根据题意判断。
【示例】
对于数组int a = [2,4,4,6,6,10,18]; 找第一个>=6的数,就是6的左边界,那么就要返回right。同理,如果要找的是右边界,那么就返回left
1 | //找到升序数组a中x第一次出现的位置 |
浮点二分:不再是在有序数组上做二分查找,而是在某个实数范围内进行查找,因为实数域本身是单调的,所以也满足单调性,和整数二分的主要区别在于使用的变量类型、退出的判断条件不同。这个知识点考的比较少,在工科数学中用到较多
1 | //计算单调函数f(x)的零点 |
在考试中的二分题很多时候看起来不是简单的有序序列或者是函数,需要读者自行从题目中分析其二分的本质
【例题】:
这题就相当具有代表性,直接看这题好像和二分一点关系都没有,但是分析可得发现当“最短跳跃距离”越长时,需要移走的石头数量也越多。于是就产生了单调性,我们通过二分“最短跳跃距离”,在已知“最短跳跃距离”的情况下容易O)计算需要搬走的石头的数量,找到分界点即可(即在至多搬走M块石头的情况下的最远跳跃距离)
在某种意义上二分和枚举是一样的思想,就是先确定所有可能值的范围,然后在里面通过一定的方法去缩小答案的范围。
本部分例题解决实现代码链接:点击此处
构造
【概念】:构造题在比赛和解决问题的过程中确实是常见的一类题型。它们通常要求解题者通过观察问题的结构和规律,找到一种通用的方法或模式,使得在问题规模增大时依然能够高效地得到答案。其思想就是数学中的构造函数、找规律。
这一部分主要侧重于读者的理解和归纳能力,由于构造方法多样且因人而异,关于其概念和方法讲解不会太多,而侧重于讲解例题加深读者对构造的理解。
【例题1】
蓝桥小蓝喜欢数学,他特别喜欢做数学题,有一天他遇到了一个有趣的数学题:
现在给定一个正整数N,小蓝想知道当x、y、z取何值时,上述等式成立。
请你帮助小蓝找到满足条件的整数x、y、z.
输入:输入包含一个正整数N(1≤N≤1000).
输出:如果存在满足条件的整数x、y、z,则输出一个满足条件的解,以空格分隔。如果有多组解,请输出任意一组即可。
如果不存在满足条件的解,则输出"No Solution"。
给出的样例如下:
样例1:
输入:
N=1
输出:
2 3 6
样例2:
输入:
N=2
输出:
4 6 12
样例3:
输入:
N=3
输出:
7 10 70
看起来好像第三项是第二项的两倍,但是当N=3的时候又不是这样,难道规律不对?其实题目中告诉你只需要找任意一个解,但出题人可不会把有规律的直接告诉你,而这个时候我们需要用数学推导以下验证我们的猜想.
当N=2时,,推导可得, x= 4,y= 6,z=12
当N=3时同理可得, x=6,y=9,z=18 看到没有,出题老登果然出一些偏数据误导你,但是只要你按照数学思维推导,还是能找到一定的规律的.
由数学归纳法得,当N = n时 即x=2n,y=3n,z=6n 证明完毕,剩下的就是将数学语言转化为计算机语言了。
总结:这类题目出题千变万化,没有通解,需要读者不断观察、猜想、证明、修正,直到找到相对准确的规律或者是构造方法。
进制转换
【概念】:每一个数位上的数字*这一位的权重(也就是进制)。
【示例】:十进制: 二进制:
常见考点
- 将任意进制转化为十进制
【思路】:从高位到低位获取每一位的数字并乘以权重+每一位的数字
1 | long long x = 0; |
数学推导
……
就是从高位开始,不断×权重+对应位的数字。
这个k进制的数组可以通过对输入字符串的处理得到,而且考题大多都是这样。
【例题】
- 1.进制 - 蓝桥云课
- 1.九进制转十进制 - 蓝桥云课 实现思路同上一题,仓库中就不展示其解答代码
- 将十进制转为任意进制
【思路】:由定义可得 可以直接计算出=x%k 。计算出来之后呢?将x/=k,然后将放在的位置上,继续执行此操作即可
1 | ll x; |
【例题】
- 1.进制转换 - 蓝桥云课 对于N进制转M进制,一个好的方法就是先将N转化为十进制,然后将十进制转化为M进制。这里就用到算法系列(一)中字符串部分字母与数字的映射关系了 忘记的赶快去看!
本部分例题解决实现代码链接:点击此处
离散化
【概念】:把无限空间中有限的个体映射到有限的空间中去,以 以此提高算法的时空效率。
离散化数组要求内部是有序 (一般是去重的,当然也存在不去重的方法, 但是比较少见)的,可以直接通过离散化下标得到值,当然也可以通过值得到离散化下标 (通过二分实现)
【示例】:比如原数组是[0,3,1000,2,9999,2],如果将值作为下标会很麻烦,将其映射到一个离散化数组中,比如[0,2,3,1000,9999] ,用离散之后的数组的下标映射原来的元素,比如下标0代表0,下标1代表2,下标2代表3……,这样就方便后续的处理
【实现】:示例如下
1 |
|
离散化数组不会单独考察,而是和其他的数据结构一起考察,常见的形式就是给定a数组,求a的离散化数组,并通过值找到其下标。
本部分例题解决实现代码链接:点击此处
枚举
【概念】:枚举算法是一种基本的算法思想,它通过穷举所有可能的情况来解决问题。它的基本思想是将问题的解空间中的每个可能的解都枚举出来,并进行验证和比较,找到满足问题条件的最优解或者所有解。人话就是穷举。
这里需要介绍以下解空间,因为很多时候枚举就是针对有限的解空间找到符合条件的解。解空间可以是 一个范围内的所有数字 (或二元组、字符串等数据),或者满足某个条件的所有数字。针对解空间的性质(比如一维数组和二维数组)选择对应的循环方法枚举所有可能的结果(比如for循环或者是嵌套循环),最终找到答案。
【例题】在蓝桥杯中考题都很简单,暴力算法足以
本部分例题解决实现代码链接:点击此处
模拟
【概念】:模拟算法通过模拟实际情况来解决问题,一般容易理解但是实现起来比较复杂,有很多需要注意的细节,或者是一些所谓很“麻烦”的东西。
【例题】
- 1.扫雷 - 蓝桥云课 还有一种解题的方法是在原有数组的基础上外加上两行两列的0,这样就不需要多层嵌套和max与min函数使用了,直接进行判断即可
- 1.灌溉 - 蓝桥云课 和上一题类似,但是要注意动态更新
- 1.回文日期 - 蓝桥云课 此题非常考验细节,涉及到数字与字符串之间的转换,日期格式的修改等,需要写多个函数实现
本部分例题解决实现代码链接:点击此处
前缀和
【概念】:prefix表示前缀和,前缀和由一个用户输入的数组生成。对于一个数组a[] (下标从1开始),我们定义一个前缀和数组prefix[],满足: .比如prefix[1]=a[1],prefix[3]=a[1]+a[2]+a[3],以此类推。
【性质】:后一项=前一项+原数组对应位的元素,即
在实际应用中prefix可以以O(1)的时间复杂度求数组a[]的一段区间的和:但是注意,prefix是一种预处理算法,只适用于a数组为静态数组的情况,即a数组中的元素在区间和查询过程中不会进行修改。
【实现】:示例如下
1 | //初始化前缀和数组 |
【例题】
本部分例题解决实现代码链接:点击此处
时空复杂度
关于其概念在数据结构中有详细的解释,没有基础的读者可以参考以下链接2.1 算法效率评估 - Hello 算法.我们主要考虑的是评测机 时间与空间的限制。
一般来说,评测机1秒大约可以跑2e8次运算,我们要尽可能地让我们的程序运算规模数量级控制在1e8以内。而题目限制的空间一般是128MB,相当于 个int,很少会有空间不足的情况,一旦出现空间不足的情况请优先考虑是否出现了栈溢出或者死循环的问题。
【示例】:斐波那契数列实现
1 |
|
时空复杂度分析:时间复杂度:每个递归调用会产生两个额外的递归调用,因此递归深度为,其中n是斐波那契数列的位置。空间复杂度:在斐波那契数列的递归算法中,递归深度为n,因此需要的堆栈空间为.注意,一般来说堆栈空间只给8MB,需要注意递归深度不宜过深,一般不宜超过1e6层,
双指针
【概念】:双指针算法是一种常用的算法技巧,它通常用于在数组或字符串中进行快速查找、匹配、排序或移动操作。其“指针”不一定是C\C++中的指针,也可以是是下标等。
常见的分类如下
对撞指针
【概念】:指的是两个指针left、right (简写为l,r)分别指向序列第一个元素和最后一个元素然后l指针不断递增,r不断递减,直到两个指针的值相撞或错开(即l>=r),或者满足其他要求的特殊条件为止。常用于解决字符串和有序数组查找相关的问题。
【例题】
- 1.回文判定 - 蓝桥云课 用双指针或者是将其反转比较均可实现
快慢指针
【概念】:指的是两个指针从同一侧开始遍历序列,且移动的步长一个快一个慢。移动快的指针被称为快指针,移动慢的指针被称为慢指针。两个指针以不同速度、不同策略移动,直到快指针移动到数组尾端,或者两指针相交,或者是其他条件
【例题】:
本部分例题解决实现代码链接:点击此处
贪心
【概念】:每一步都选择局部最优解,而尽量不考虑对后续的影响,最终达到全局最优解。贪心是一种算法思想而不是一种具体的数据结构或者是构造。
【实现】:参考的解答步骤如下
- 确定问题的最优子结构(贪心往往和排序、优先队列等一起出现)。
- 构建贪心选择的策略,可能通过“分类讨论”、“最小代价”、“最大价值”等方式来思考贪心策略。简单验证贪心的正确性,采用句式一般是:这样做一定不会使得结果变差、不存在比当前方案更好的方案等等。
- 通过贪心选择逐步求解问题,直到得到最终解。
【例题】
- 1.最小化战斗力差距 - 蓝桥云课
- 1.谈判 - 蓝桥云课 使用了优先级队列,当然用栈的话也是一样的道理
- 1.纪念品分组 - 蓝桥云课 使用了双指针的小技巧
本部分例题解决实现代码链接:点击此处
位运算
【概念】:位运算是一种对二进制数的位进行操作的运算方式。它直接对二进制数的每一位进行逻辑操作,而不考虑整个数的数值大小,一般情况下,位运算中每一位都相互独立,各自运算得出结果 (左右移除外)
一般情况下位运算只能应用于整数(而且一般是非负数),而且在计算机中整数是以补码的形式存储的,而正数的源码=补码。
以下知识在《数字电路技术》中有详细的解释,这里主要讲解算法中常用的部分
按位与and(&)
两个位为1时才为1。
【性质】:两个数字做与运算,结果不会变大
按位或or(|)
有一个位为1时就为1。
【性质】:两个数字做或运算,结果不会变小
按位异或xor(^)
两个位不同时为1,相同为0。
异或的性质
| 规律 | 公式 |
|---|---|
| 交换律 | |
| 结合律 | |
| 自反性 | |
| 零元素 | |
| 逆运算 | 则有 两边同时异或y,低消掉 |
按位取反(~)
0变成1,1变成0。
一般情况下用于无符号整数,避免符号位取反。
按位左移(<<)
左移(<<)操作将一个数的二进制表示向左移动指定的位数。移动后,低位补0,如果数据类型为有符号整型,注意移动的时候不要移动到符号位上,或者干脆使用无符号整型。1会移动到符号位.
【性质】:左移操作相当于对原数进行乘以2的幂次方的操作。比如5<<3 相当于
按位左移(<<)
右移(>>)操作将一个数的二进制表示向右移动指定的位数。移动后,一般情况高位补0,如果数据类型为有符号整型,注意移动的时候让符号位为0,或者干脆使用无符号整型。如果符号位上有1不会被移走,这是负数位移的规则
【性质】:右移操作相当于对原数进行除以2的幂次方的操作。比如5>>3 相当于 5 ÷ 并向下取整
按位设置
C++代码示例如下
1 |
|
位运算的应用
- 判断奇偶性:x&1,结果是1说明是奇数,0为偶数。原理就是判断最后一个位是1还是0.
- 获取二进制某一位:x>>i&1结果必然为0或1,表示x的二进制表示中的第i位。
- 修改二进制中的某一位为1: x I (1 << i)将x的第i位或上1,则x[i]变为1,其他位上或上0没有影响。如果读者做的题够多的话,会发现这个方法和字符型字母大小写转换是类似的,在倒数第6位修改为1可以实现大写转小写(原理,字母大写与小写相差32)
- 快速判断一个数字是否为2的幂次方:X & (x- 1) 如果x为2的幕次方,则x的二进制表示中只有一个1,X-1就有很多个连续的1并且和x的1没有交集,两者与运算一定为0,可以证明其他情况必然不为0。
- 获取二进制位中最低位的1:lowbit(x) =x & -x 如果x=(010010),则lowbit(x)=(000010).常用于数据结构树状数组中。
- ……
【例题】
本部分例题解决实现代码链接:点击此处
排序
在实际解决题目的时候一般要求掌握排序的使用方法(比如C++中的sort),而不会侧重于排序的实现。
插入排序
【概念】:插入排序是一种简单直观的排序算法,其基本思想是将待排序的元素逐个插入到已排序序列的合适位置中,使得已排序序列逐渐扩大,从而逐步构建有序序列,最终得到完全有序的序列。生活中的例子就是打扑克牌
【实现】:就是插入+移动
1 | //i表示当前要确定的位置 |
【例题】:
- 1.宝藏排序Ⅰ - 蓝桥云课 如果你知道C++中的sort,这题就直接秒了o( ̄▽ ̄)o
本部分例题解决实现代码链接:点击此处
归并排序
【概念】:原理是将一个数组分成两个子数组,将子数组向下递归的排序后(当数组中仅有一个元素值无需再排序了,直接返回),得到两个有序数组,然后进行O(n)的合并,最终合并成有序的原数组。
【实现】:先递归实现两边分别有序,然后一点点排序
1 |
|
【例题】
- 1.宝藏排序Ⅱ - 蓝桥云课 尝试用归并排序的方法实现
本部分例题解决实现代码链接:点击此处 注意文件名为lanqiao_3226_MergeSort表明此题是用归并排序实现的
快速排序
【概念】:快速排序是一种基于分治法的排序方法,原理是将一个数组分成两个子数组,其中一个子数组的所有元素都小于另一个子数组的元素,然后递归地对这两个子数组进行排序。
【实现】:
1 |
|
【例题】
- 1.宝藏排序Ⅱ - 蓝桥云课 尝试用快速排序的方法实现
本部分例题解决实现代码链接:点击此处
冒泡排序
【概念】:冒泡排序的思想是每次将最大的一下一下运到最右边,然后将最右边这个确定下来,再来确定第二大的,再确定第三大的。算是排序中比较容易实现的算法,但是其复杂度过高,在较多元素排序的情况下会有超时的风险。
【实现】:
1 |
|
【例题】:
- 1.宝藏排序Ⅰ - 蓝桥云课 这里为什么没有用3226题作为例题呢?因为排序的数据有1e5次方,如果使用冒泡排序就会超时,所以冒泡排序只适合数据量较少的情况。
本部分例题解决实现代码链接:点击此处
桶排序
【概念】:桶排序(Bucket sort)是一种非比较的排序算法。桶排序采用了一些分类和分治的思想,把元素的值域分成若干段,每一段对应一个桶。在排序的时候,首先把每一个元素放到其对应的桶中,再对每一个桶中的元素分别排序,再按顺序把每个桶中的元素依次取出,合并成最终答案。
【实现】:此算法与归并排序十分相似,不同的是这里的分段不完全像归并一样递归到1个元素的排序,而可能是多个元素的。还有就是排序的时候没有比较,算法的时间复杂度小,但是用空间换来的。步骤如下
- 将值域分成若干段,每段对应一个桶
- 将待排序元素放入对应的桶中
- 将个桶内的元素进行排序
- 将桶中的元素依次取出
1 | //题目链接: https://www.lanqiao.cn/problems/1314/learning/?page=1&first_category_id=1&problem_id=1314 |
在元素值较小的情况下当然可以这样为每一个值分配一个桶,但是如果值可以是1e9甚至更多呢?那么就必须要将其分段然后排序了
1 | //题目链接: https://www.lanqiao.cn/problems/1314/learning/?page=1&first_category_id=1&problem_id=1314 |
总结:对于数据量较大但值域较小的数据,如,可以做到每个值对应一个桶,桶排序的时间复杂度为O(n)。推荐使用桶排序。
选择排序
【概念】:选择排序的思想和冒泡排序类似,是每次找出最大的然后直接放到右边对应位置,然后将最右边这个确定下来(而不是一个一个地交换过去)。
【实现】:
1 |
|
【例题】
本部分例题解决实现代码链接:点击此处
参考
- 力扣刷题攻略 读者可以在这里参考刷题。
- 蓝桥云课C++班,作者谢子杨






